Polytope im IR 4 (= Polychora)
|
Start Historisches Definitionen Platonische Polychora Archimedische Polychora antiprismat. Prismachora Biprismachora Beweise Links Kontakt Alle Abbildungen auf dieser Seite sind Java-Applets, die sich - einmal geladen - mit der Maus drehen lassen. | |
|
optimiert f r Mozilla Firefox 2.0 Stand April 2008 |
p,q-Biprismachora
Um p,q-Biprismachora
zu erzeugen, müssen wir uns mit deren Abwicklungen ein wenig näher beschäftigen.
Stellen wir uns ein p-Prisma (p ≥ 3) vor, das vor uns auf
einem seiner p-Ecke auf dem Tisch liegt. Jetzt legen wir weitere p-Prismen,
jeweils p-Eck auf p-Eck darauf, bis ein Turm von q Prismen
(q ≥ 3) entsteht. Betrachten wir jetzt nur einen von p
senkrechten Streifen, der aus q Quadraten besteht und der vom unteren
Prisma bis zum oberen verläuft. Diesen Streifen können wir gedanklich vom Turm
lösen und flach auf den Tisch legen. Jetzt ist es offensichtlich, dass wir
diesen Streifen zu einem mehr oder weniger eckigen Ring aus q Quadraten
zusammenrollen können, indem wir entlang der Kanten zwischen den 4-Ecken nach
oben (senkrecht zur Streifen-Ebene) knicken und die freie Kante des ersten mit
der freien Kante des letzten 4-Ecks zusammenkleben. Sind alle Knickwinkel
gleich, erhalten wir ein regelmäßiges q-Prisma.
Kommen wir jetzt wieder zurück
zu unserem Turm. Nun können wir jeden der p Streifen zu einem q-Prisma
aufrollen. Versuchen wir es allerdings simultan, dann zerreißen wir im
Anschauungsraum die p-Ecke des Turmes. Wenn wir aber die Richtungen, in
die wir die Streifen aufrollen, so wählen, dass wir nicht nur senkrecht zur
Streifen-Ebene, sondern sogar senkrecht zum Turm (bzw. dessen 3-dimensionaler
Hyperebene) knicken, dann wird klar, dass wir den Turm selbst auch aufrollen
und dass dessen Deckel-p-Eck (die obere Fläche des Turmes) nun zusammenfällt
mit der Grundfläche, auf der der Turm steht. Dies ist insbesondere deshalb
einleuchtend, da diese p-Ecke aus p Kanten bestehen, die alle
gleichzeitig, jeder in seinem Streifen, mit der entsprechenden Kante des
unteren p-Ecks zusammenkommen. Wir erhalten also aus dem Turm einen Ring
von q gleichen p-Prismen und aus den Streifen einen Ring aus p
gleichen q-Prismen, wobei beide Ringe senkrecht zueinander stehen und
nur über 4-Ecke miteinander verbunden sind. Deshalb nennen wir diese Polychora
auch p,q-Biprismachora (p,q ≥ 3).
Diese Polychora sind
selbstverständlich uniform: An jeder Ecke liegen zwei p-Prismen (vom
Turm) und zwei q-Prismen (von den Streifen). Als Sonderfall dieser
Biprismachora haben wir für p = q = 4 den 8-Zeller. Da haben wir nämlich
folgende Situation: Einem 4-Prisma geben wir die vierte Koordinate Null,
parallel dazu einem zweiten 4-Prisma die vierte Koordinate k (k
sei die Kantenlänge). Dann bilden die beiden korrespondierenden 4-Eckpaare zwei
weitere 4-Prismen (also sind es jetzt insgesamt vier) und die vier 4er-Streifen
werden zu vier 4-Prismen (=Hexaeder). Damit ist also die Klasse von unendlichen
Prismachora – nämlich die mit Prismen als Basis anders die mit Antiprismen als
Basis – nur ein Teil dieser Biprismachor-Klasse.
|
|
|
|
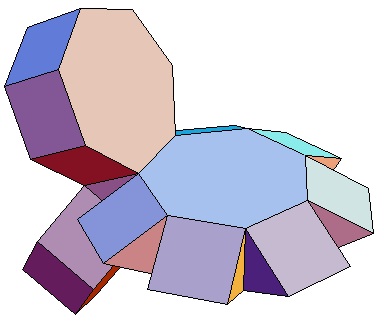
|
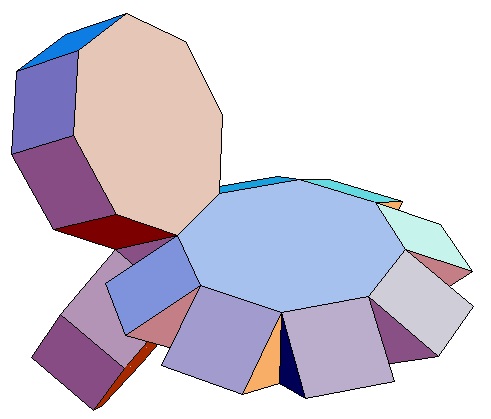
|
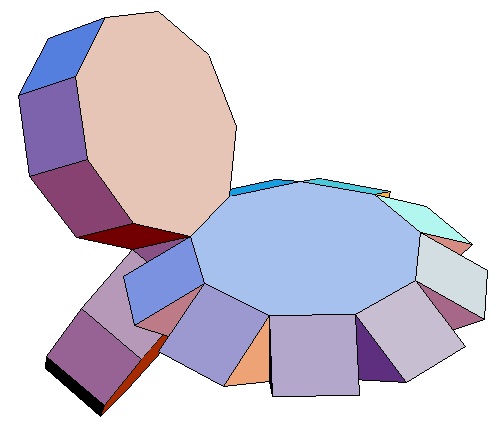
|
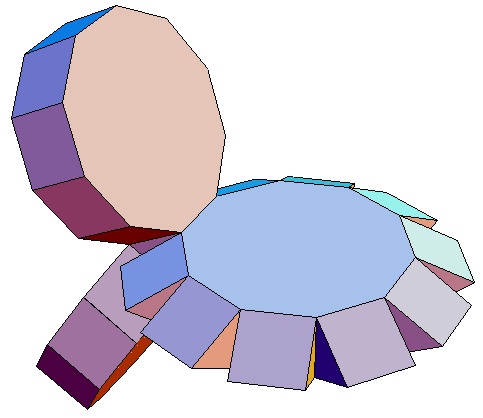
|
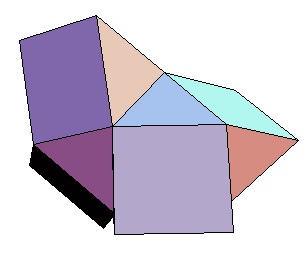
| Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung |
| des 3,3-Bipris- | des 3,4-Bipris- | des 3,5-Bipris- | des 3,6-Bipris- | des 3,7-Bipris- | des 3,8-Bipris- | des 3,9-Bipris- | des 3,10-Bipris- |
| machors | machors | machors | machors | machors | machors | machors | machors |
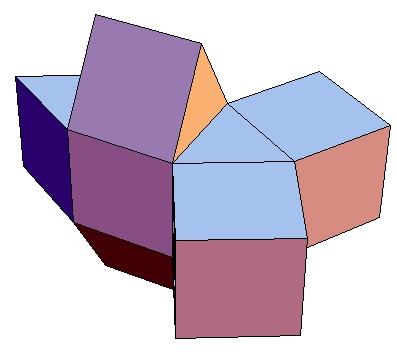
|
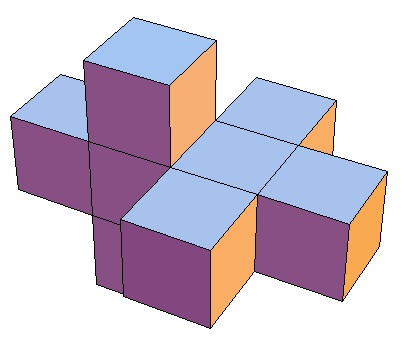
|
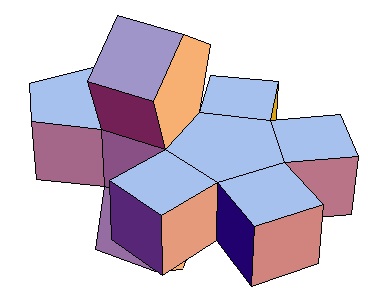
|
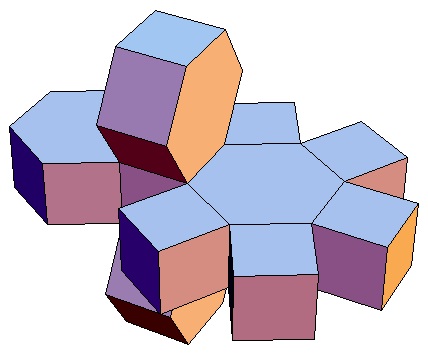
|
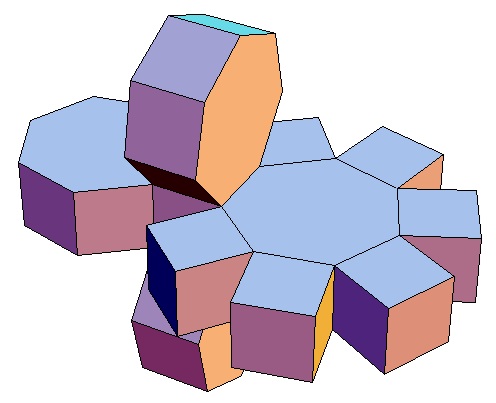
|
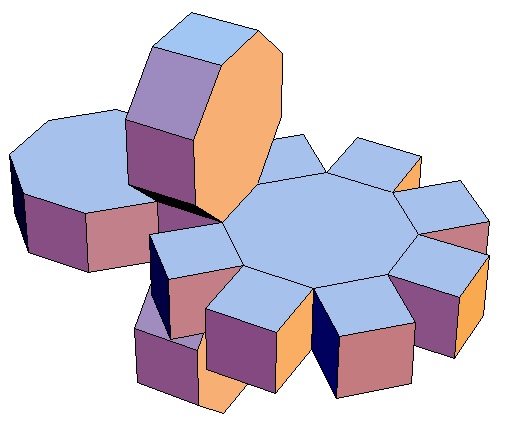
|
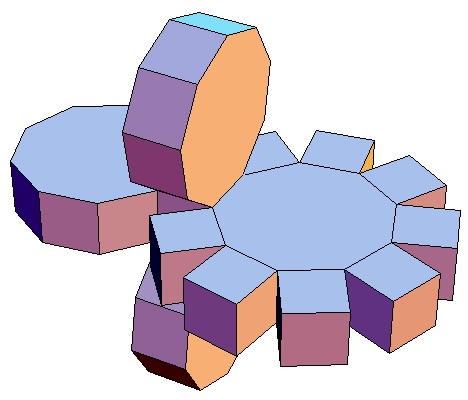
|
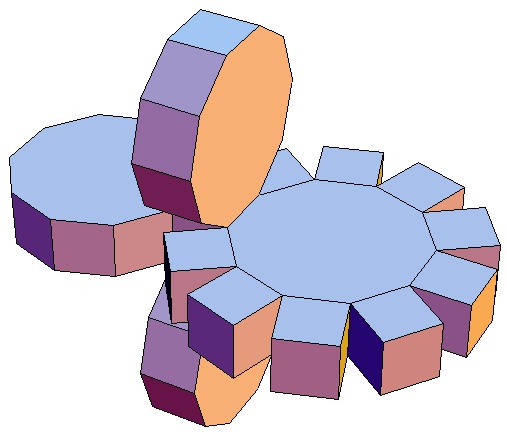
|
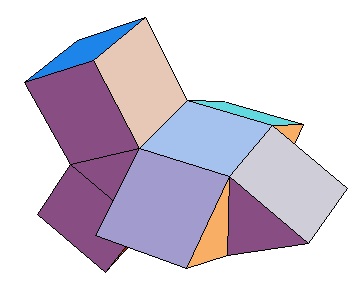
| Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung |
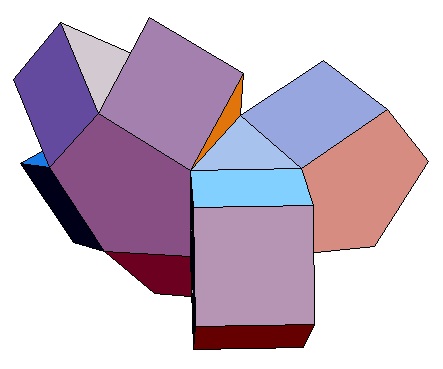
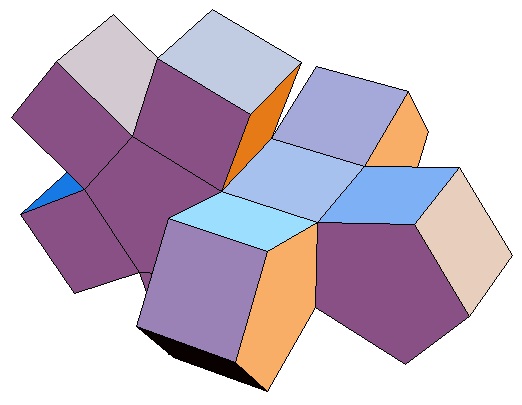
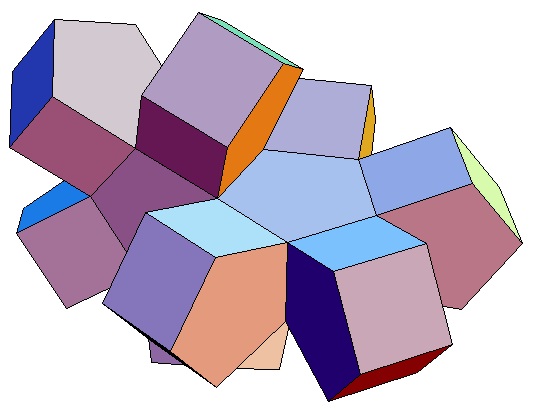
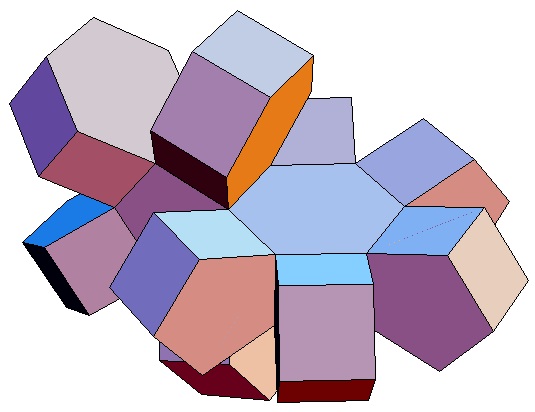
| des 4,3-Bipris- | des 4,4-Bipris- | des 4,5-Bipris- | des 4,6-Bipris- | des 4,7-Bipris- | des 4,8-Bipris- | des 4,9-Bipris- | des 4,10-Bipris- |
| machors | machors | machors | machors | machors | machors | machors | machors |
| oder 8-Zellers | |||||||
|
|
|
|
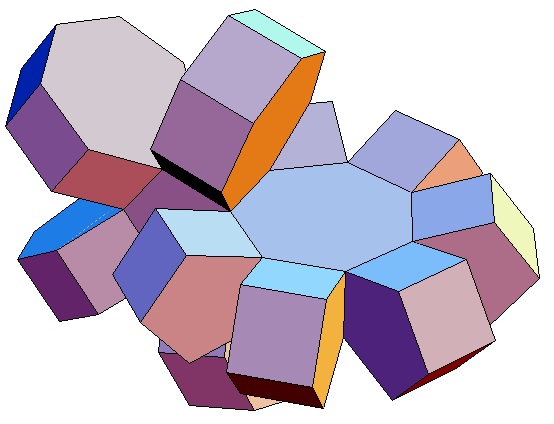
|
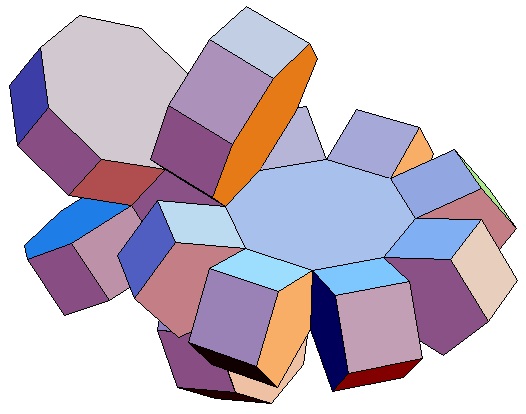
|
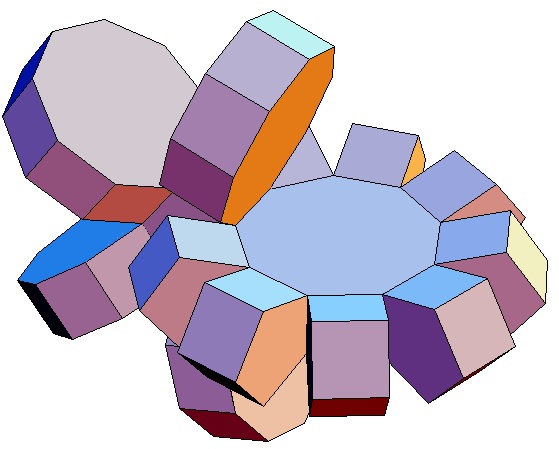
|
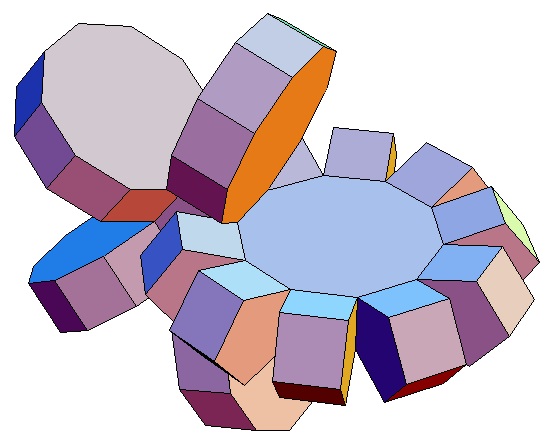
|
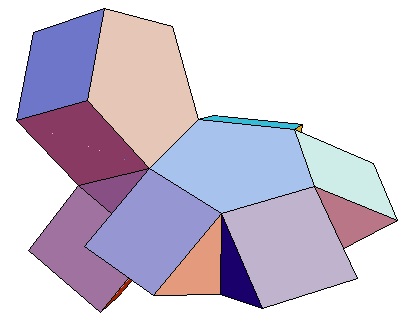
| Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung |
| des 5,3-Bipris- | des 5,4-Bipris- | des 5,5-Bipris- | des 5,6-Bipris- | des 5,7-Bipris- | des 5,8-Bipris- | des 5,9-Bipris- | des 5,10-Bipris- |
| machors | machors | machors | machors | machors | machors | machors | machors |
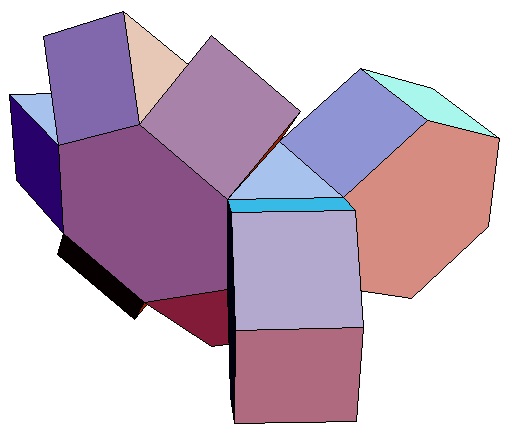
|
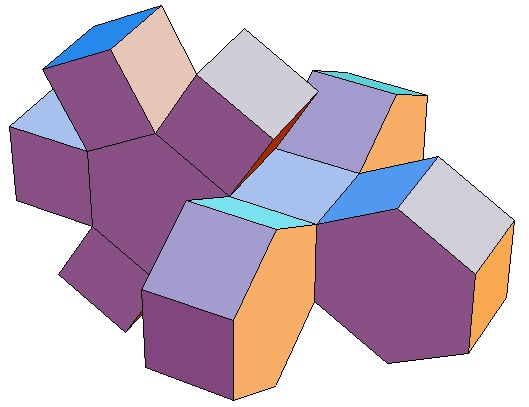
|
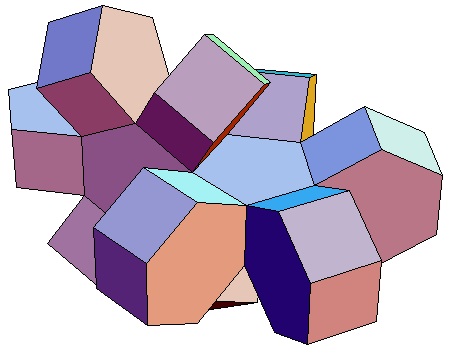
|
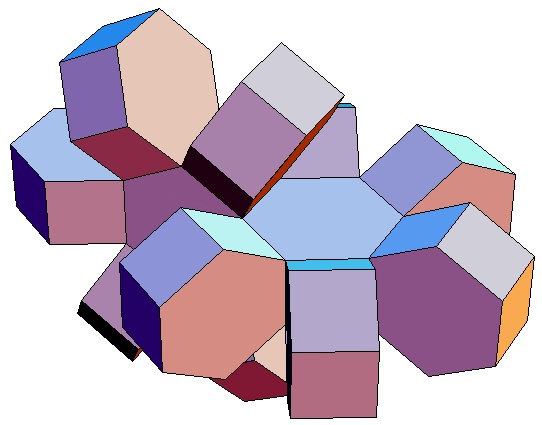
|
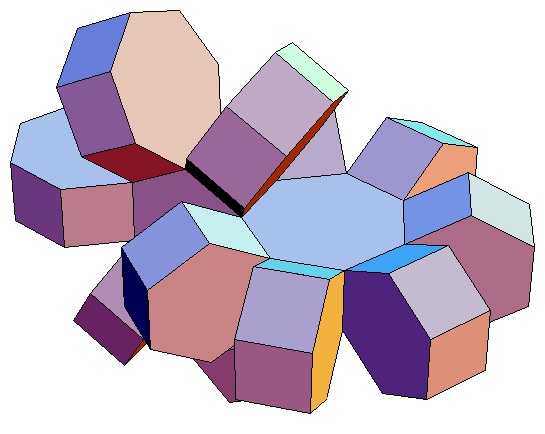
|
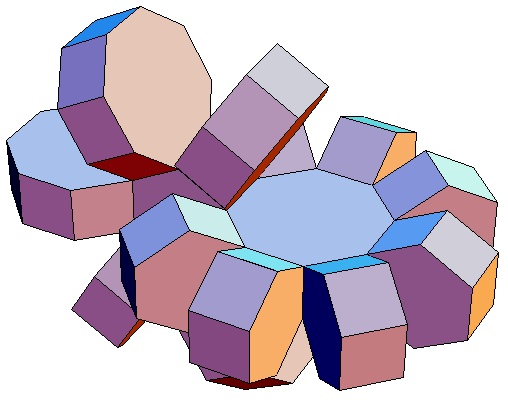
|
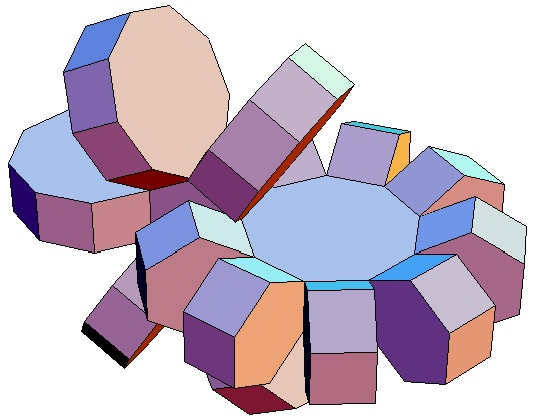
|
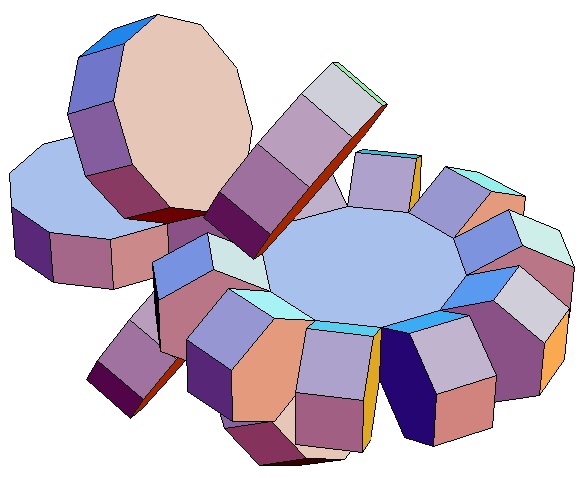
|
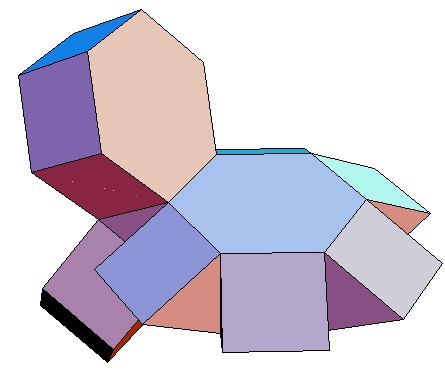
| Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung |
| des 6,3-Bipris- | des 6,4-Bipris- | des 6,5-Bipris- | des 6,6-Bipris- | des 6,7-Bipris- | des 6,8-Bipris- | des 6,9-Bipris- | des 6,10-Bipris- |
| machors | machors | machors | machors | machors | machors | machors | machors |
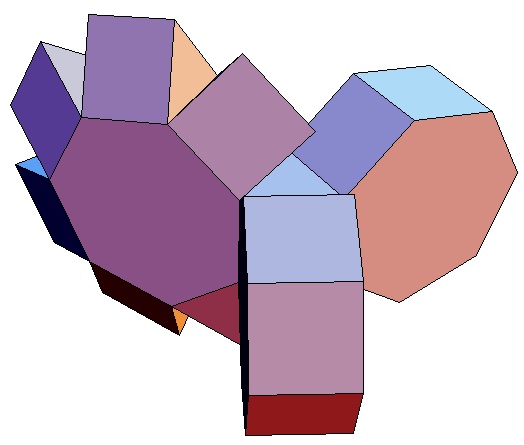
|
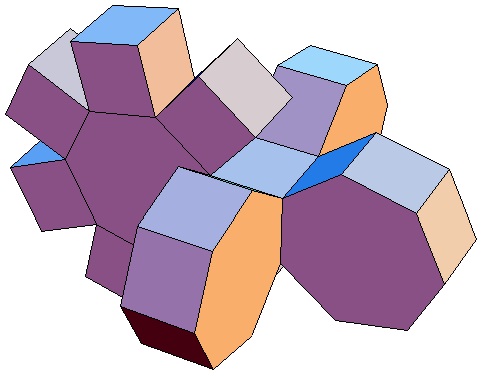
|
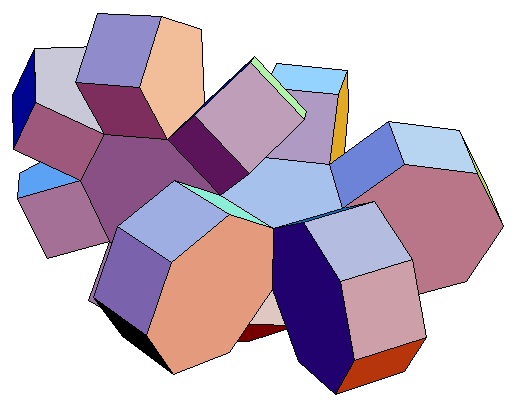
|
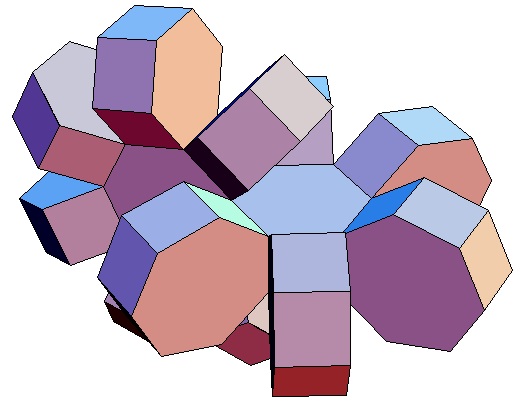
|
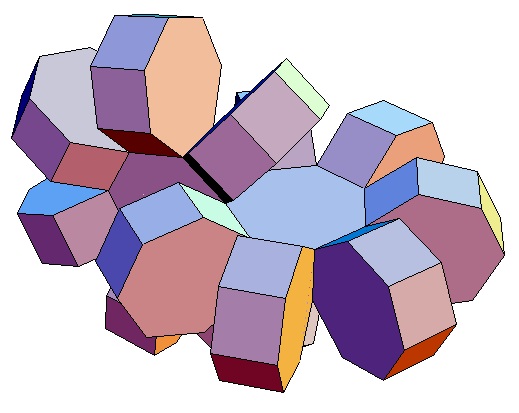
|
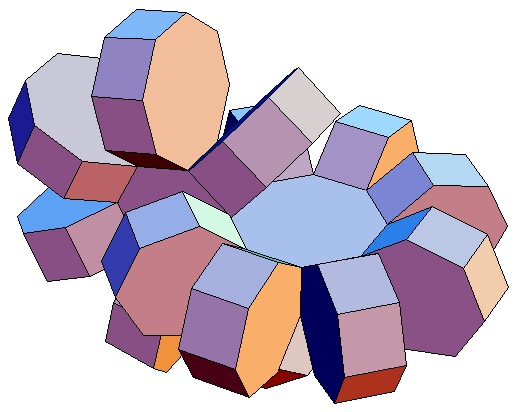
|
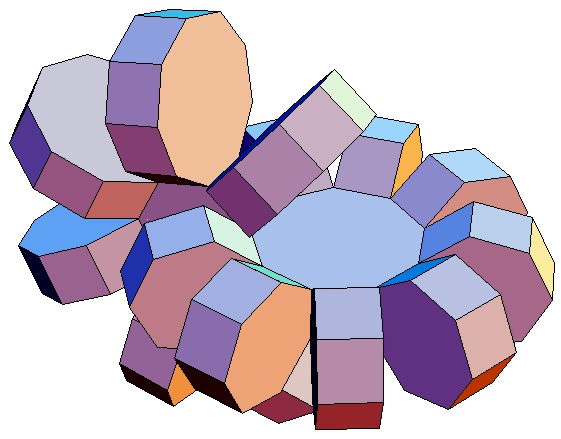
|
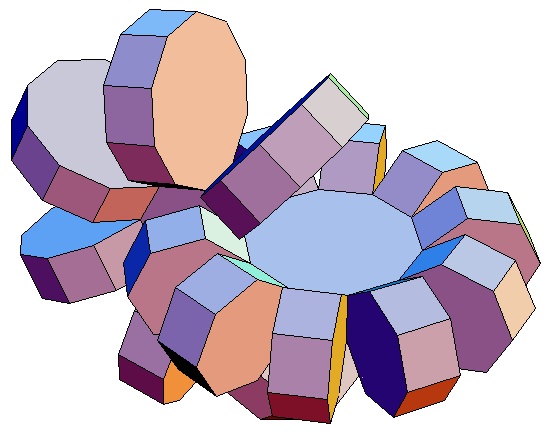
|
| Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung |
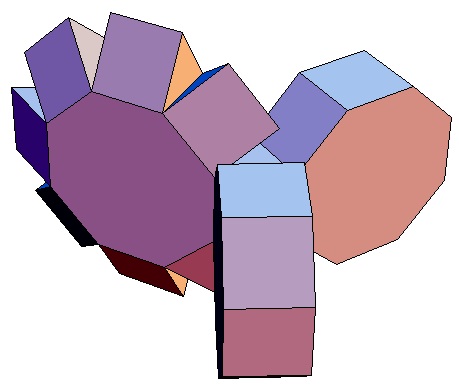
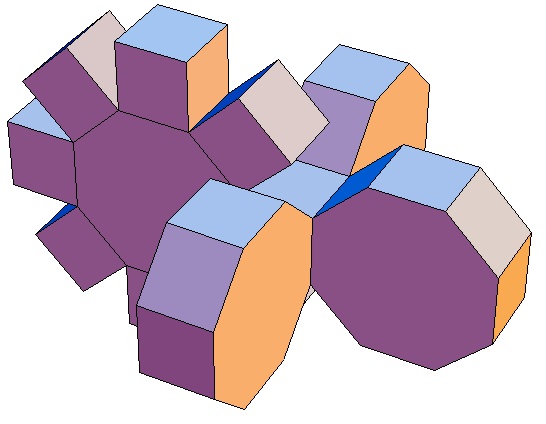
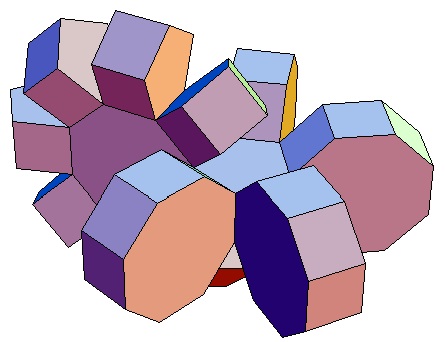
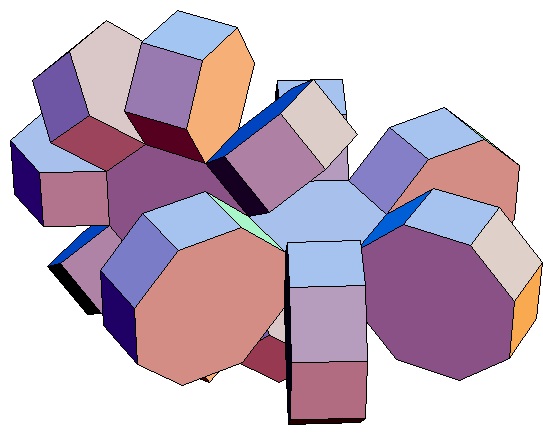
| des 7,3-Bipris- | des 7,4-Bipris- | des 7,5-Bipris- | des 7,6-Bipris- | des 7,7-Bipris- | des 7,8-Bipris- | des 7,9-Bipris- | des 7,10-Bipris- |
| machors | machors | machors | machors | machors | machors | machors | machors |
|
|
|
|
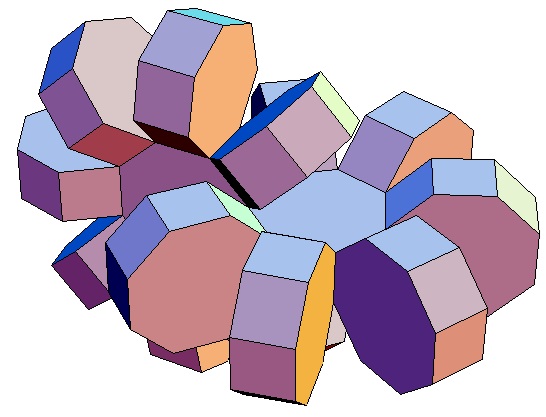
|
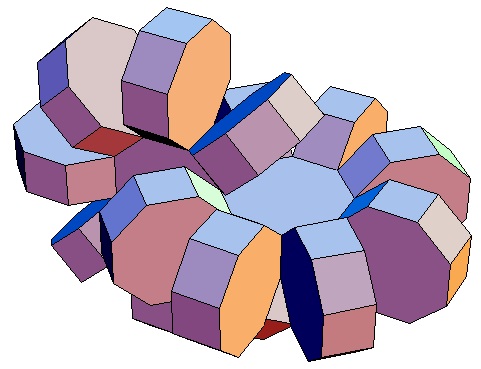
|
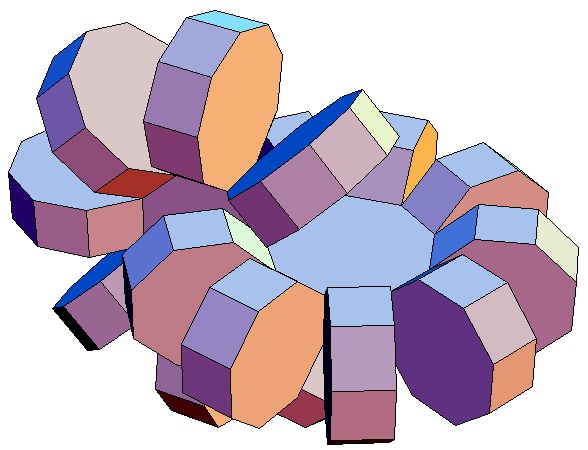
|
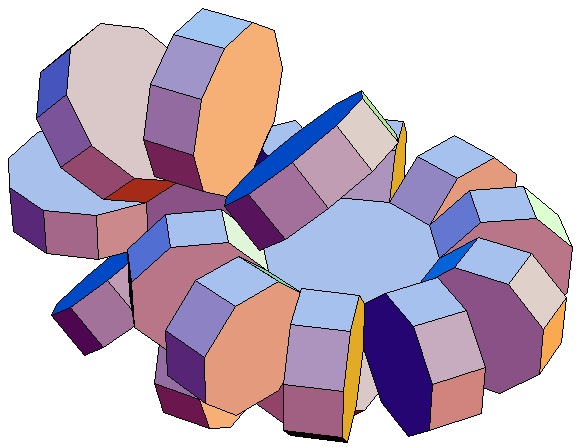
|
| Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung |
| des 8,3-Bipris- | des 8,4-Bipris- | des 8,5-Bipris- | des 8,6-Bipris- | des 8,7-Bipris- | des 8,8-Bipris- | des 8,9-Bipris- | des 8,10-Bipris- |
| machors | machors | machors | machors | machors | machors | machors | machors |
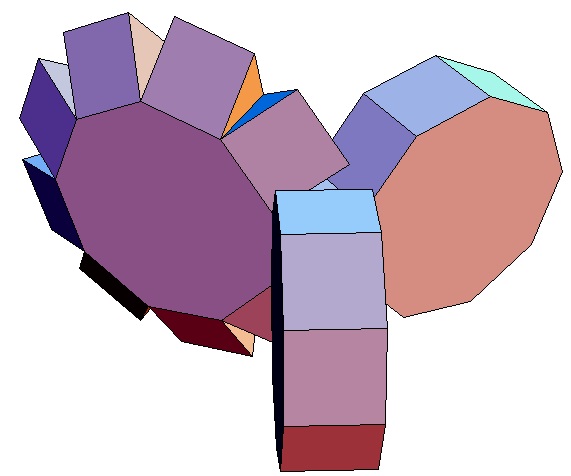
|
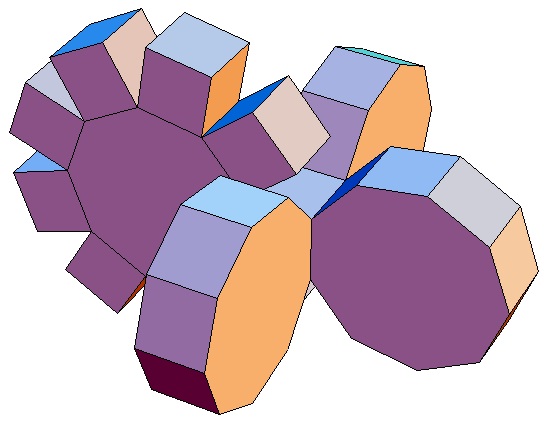
|
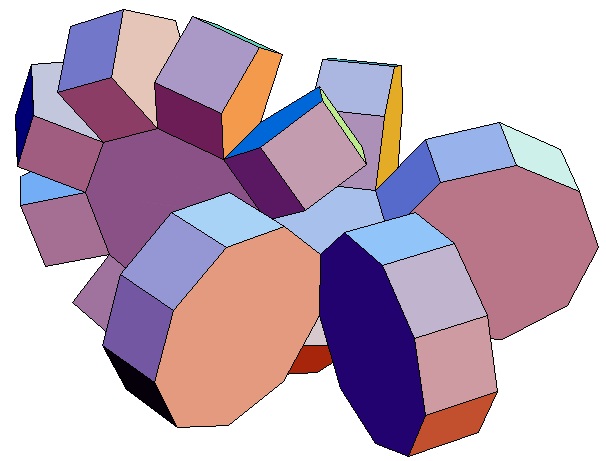
|
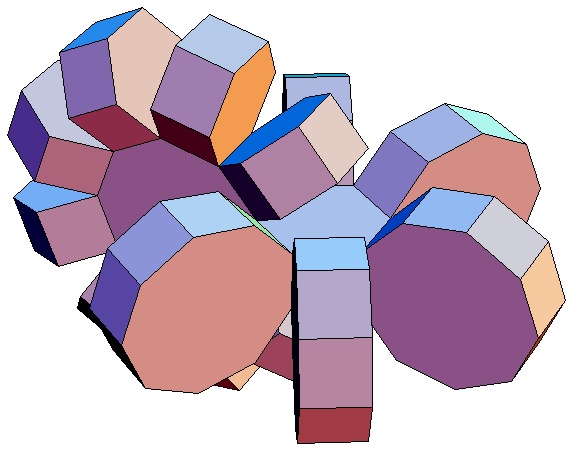
|
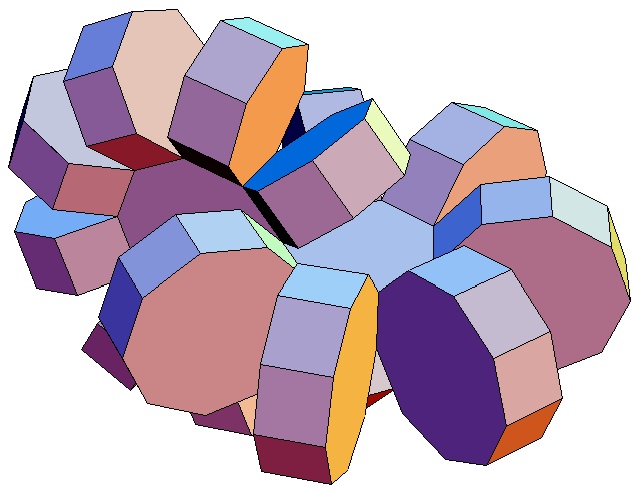
|
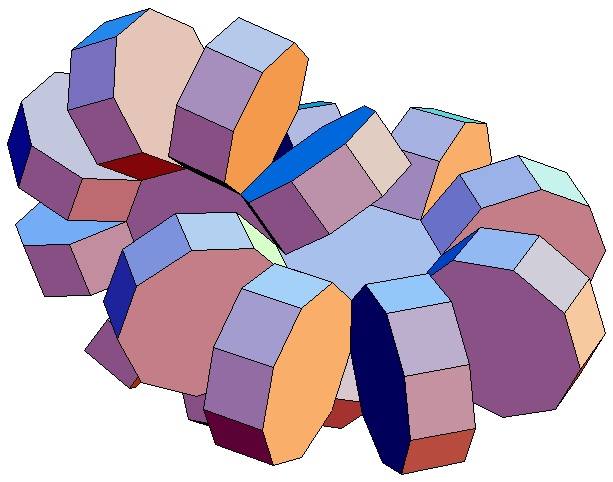
|
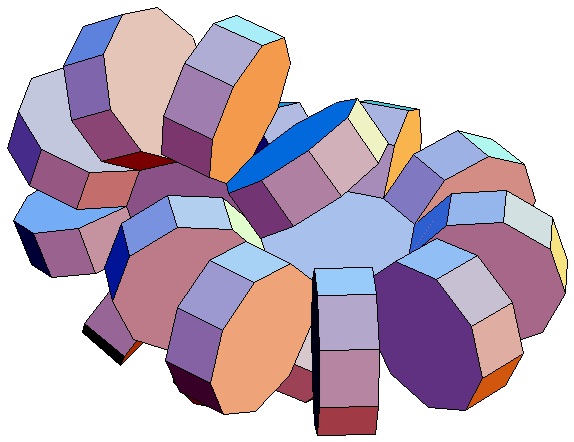
|
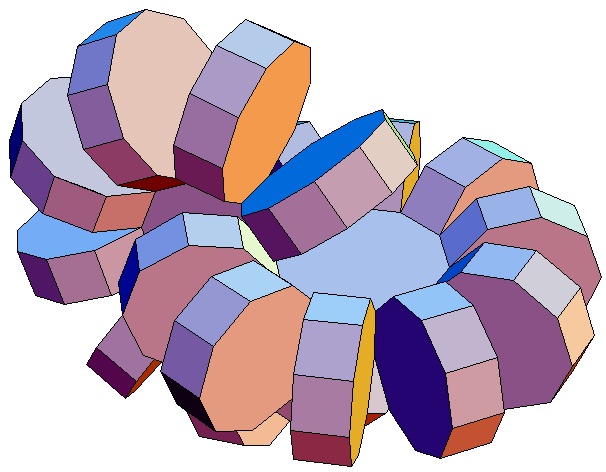
|
| Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung |
| des 9,3-Bipris- | des 9,4-Bipris- | des 9,5-Bipris- | des 9,6-Bipris- | des 9,7-Bipris- | des 9,8-Bipris- | des 9,9-Bipris- | des 9,10-Bipris- |
| machors | machors | machors | machors | machors | machors | machors | machors |
|
|
|
|
|
|
|
|
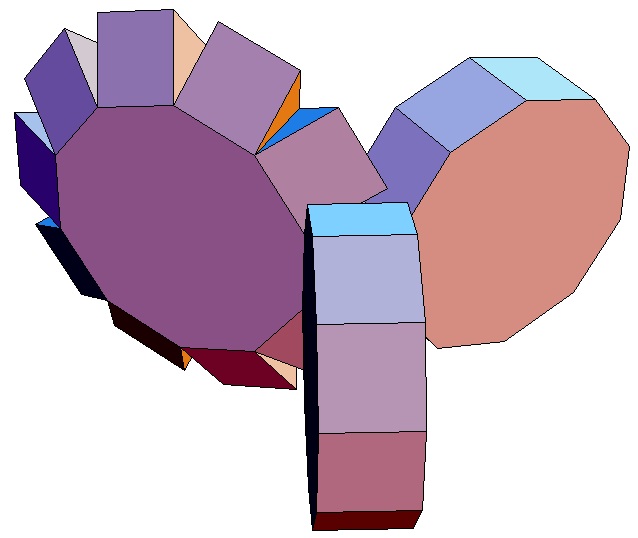
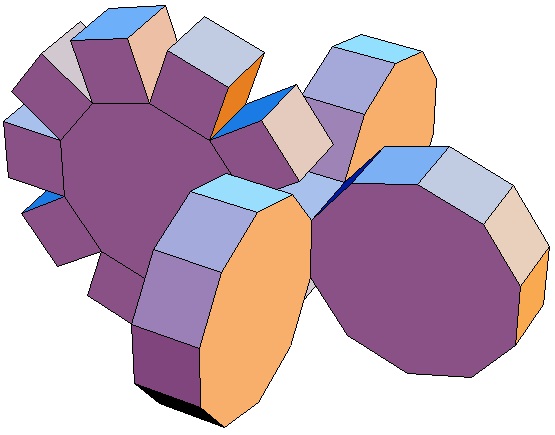
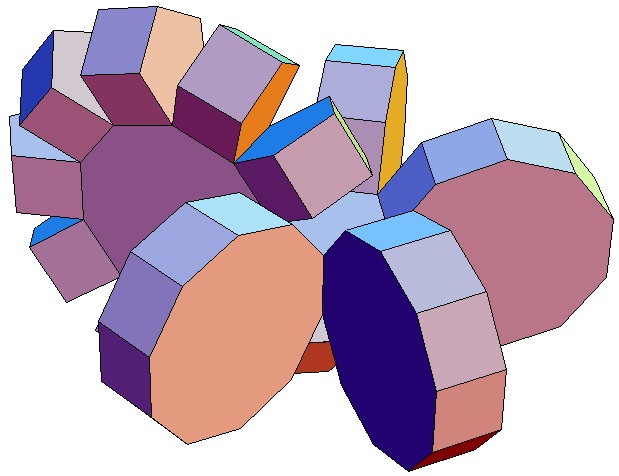
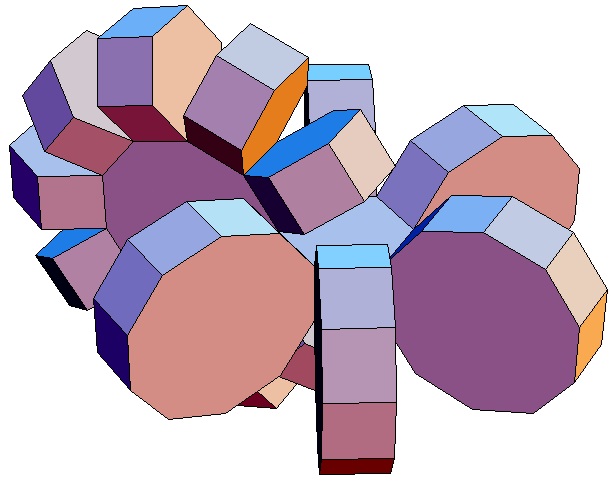
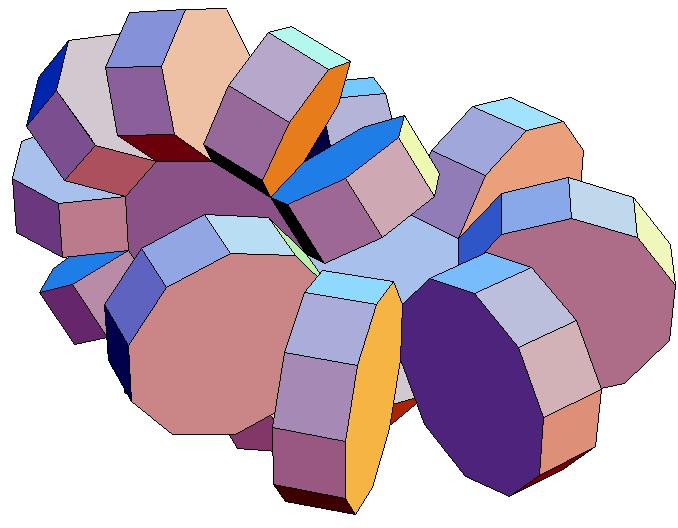
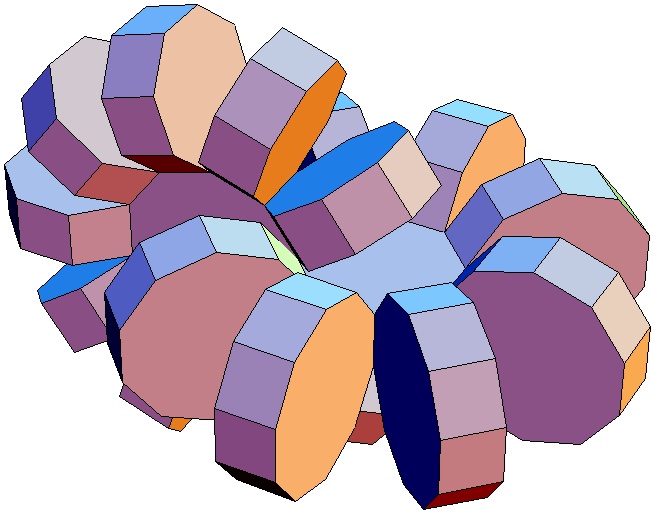
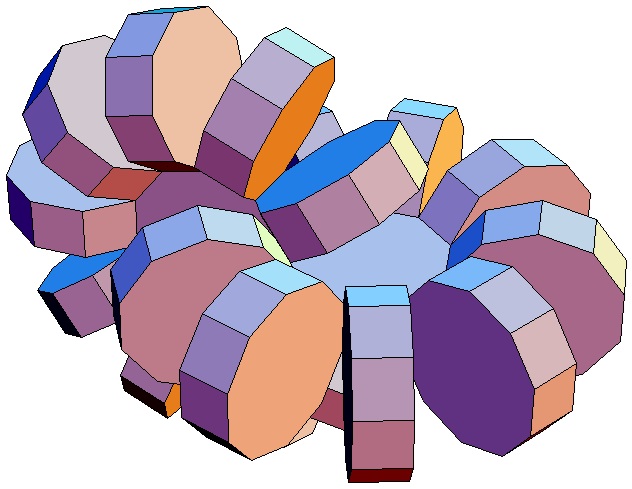
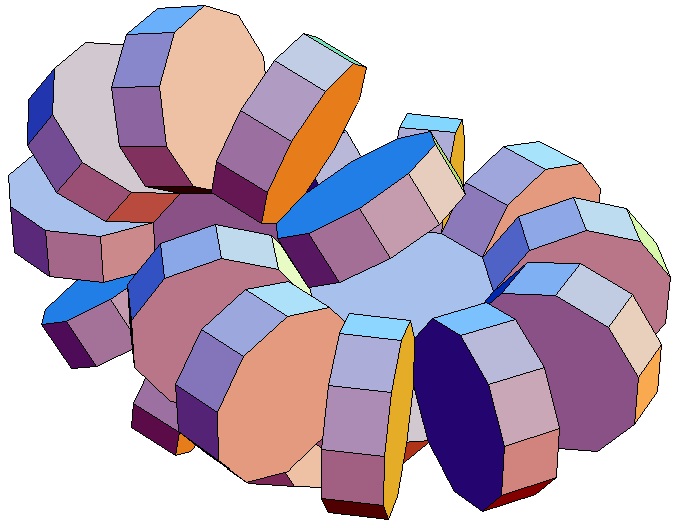
| Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung | Abwicklung |
| des 10,3-Bipris- | des 10,4-Bipris- | des 10,5-Bipris- | des 10,6-Bipris- | des 10,7-Bipris- | des 10,8-Bipris- | des 10,9-Bipris- | des 10,10-Bipris- |
| machors | machors | machors | machors | machors | machors | machors | machors |
Hier sind nur die Biprismachora von
p = q = 3
bis p = q = 10 abgebildet. Selbstverständlich gibt
es für alle p,q ≥ 3 ein p,q-Biprismachor.
Und klar ist auch, dass ein
p,q- und q,p-Biprismachor auch identisch und nur die Darstellungen
gedreht sind. Für eine wachsende Variable (und kleiner anderer) nähert sich das Polychor einer
3-dimensionalen Scheibe mit Dicke im IR 4;
für wachsende p und q ähnelt das Polychor immer mehr der
4-dimensionalen Sphäre.